UNIDAD15
UNIDAD 15 - ÓPTICA GEOMÉTRICA
La óptica geométrica es la parte de la Física que estudia, mediante leyes geométricas sencillas, los cambios de dirección que experimentan los rayos de luz en la reflexión y la refracción. En este apartado vamos a estudiar los fundamentos de la óptica geométrica. Para ello explicaremos:
Históricamente, el desarrollo y la aplicación de la óptica discurrió al margen de las discusiones sobre la naturaleza de la luz, ya que los principios sobre los que esta se estructuró son compartidos por los modelos ondulatorio y corpuscular. Veámoslos.
Recuerda que un rayo no es un haz de luz, que físicamente sí existe
(aunque las leyes de la óptica suelen ilustrarse en los laboratorios
mediante haces finos).
ndependencia de los rayos
 Este principio se puede extender a sistemas complejos como el de la figura:
Este principio se puede extender a sistemas complejos como el de la figura:
 Cada una de estas formas se hace corresponder con un determinado signo, positivo o negativo, del radio R. Esto dependerá del criterio de signos elegido. Nosotros te recomendamos que utilices el criterio DIN ( iniciales de Deutsches Institut for Normung o Instituto Alemán de Normalización ):
Cada una de estas formas se hace corresponder con un determinado signo, positivo o negativo, del radio R. Esto dependerá del criterio de signos elegido. Nosotros te recomendamos que utilices el criterio DIN ( iniciales de Deutsches Institut for Normung o Instituto Alemán de Normalización ):
 El objetivo principal de los sistemas ópticos es la formación de
imágenes. Cuando todos los rayos de un objeto puntual que pasan por el
sistema óptico convergen en un punto, decimos que dicho punto es la imagen
del objeto. En el caso de los objetos no puntuales, los distintos
puntos de la superficie del mismo convergerán en distintos puntos de la
imagen formando una réplica del objeto original. La imagen puede ser
clasificada:
El objetivo principal de los sistemas ópticos es la formación de
imágenes. Cuando todos los rayos de un objeto puntual que pasan por el
sistema óptico convergen en un punto, decimos que dicho punto es la imagen
del objeto. En el caso de los objetos no puntuales, los distintos
puntos de la superficie del mismo convergerán en distintos puntos de la
imagen formando una réplica del objeto original. La imagen puede ser
clasificada:
 En este nivel nos centraremos en el estudio de objetos simples que
representaremos en los ejercicios, normalmente, con forma de flecha.
Así, aunque cada punto del objeto es fuente de infinitos rayos, para
determinar la posición de la imagen bastará, por lo general, considerar
sólo los rayos más importantes, que llamaremos rayos significativos.
En este nivel nos centraremos en el estudio de objetos simples que
representaremos en los ejercicios, normalmente, con forma de flecha.
Así, aunque cada punto del objeto es fuente de infinitos rayos, para
determinar la posición de la imagen bastará, por lo general, considerar
sólo los rayos más importantes, que llamaremos rayos significativos.
La óptica geométrica es la parte de la Física que estudia, mediante leyes geométricas sencillas, los cambios de dirección que experimentan los rayos de luz en la reflexión y la refracción. En este apartado vamos a estudiar los fundamentos de la óptica geométrica. Para ello explicaremos:
- Algunos supuestos que sirven de base para sustentar la teoría de la óptica geométrica
- Los conceptos con los que debes familiarizarte para analizar un sistema óptico
Aproximaciones previas
La óptica geométrica se basa en una serie de nociones y principios fundamentales a partir de los cuales puede deducirse el comportamiento de distintos instrumentos ópticos a los que estamos acostumbrados, como gafas, cámaras fotográficas, telescopios, espejos, o el propio ojo humano.Históricamente, el desarrollo y la aplicación de la óptica discurrió al margen de las discusiones sobre la naturaleza de la luz, ya que los principios sobre los que esta se estructuró son compartidos por los modelos ondulatorio y corpuscular. Veámoslos.
Rayos
Los rayos son líneas rectas que indican, mediante una flecha, la dirección y sentido de propagación de la onda. La óptica geométrica se basa en la aproximación del rayo pero no debemos olvidar que se trata sólo de una construcción matemática.
Rayos y frentes de onda
Los rayos, en rojo, son perpendiculares a los frentes de onda,
en azul, en cada uno de sus puntos. Mediante los rayos representamos en
realidad la dirección de propagación del flujo de energía radiante.
Las leyes de la óptica geométrica
Propagación rectilínea de la luz
Este principio supone que los rayos de luz se propagan en línea recta y con la misma velocidad en todos los puntos y en todas las direcciones. Para ello debe cumplirse:- Que las dimensiones de los objetos sean mucho mayores que la longitud de onda de la luz. De esta manera, no se produce difracción
- Que el medio de propagación sea homogéneo e isótropo
Propagación rectilínea de la luz
La formación de sombras dio lugar, ya desde la Antigüedad, a la idea
de que la luz se propaga en línea recta. En la figura puede apreciarse
como el tamaño de la sombra de la bola sobre el suelo es el mismo que el
que se obtendría prolongando geométricamente rectas que partiesen del
foco y pasasen por los puntos del contorno del objeto.
Independencia de los rayos
Este supuesto establece que cada rayo es independiente de los demas y no interfieren entre sí.ndependencia de los rayos
A la izquieda, fotografía de un paisaje. A la derecha, fotografía
similar en la que se han bloqueado ciertos rayos con una cartulina En la
figura derecha se pone de manifiesto que el resultado obtenido para la porción de paisaje no tapada es
el mismo que el que obtienes, para dicha parte del paisaje, cuando no
has tapado nada. Esto se debe, precisamente, a que los rayos que tapamos
en la segunda fotografía eran independientes del resto, que se
comportan igual en ambos casos, formando la misma imagen.
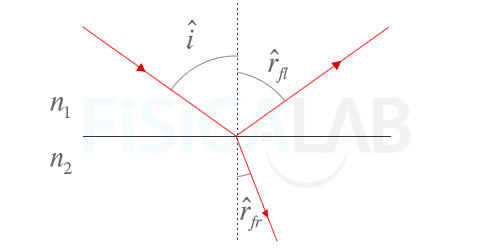
Reflexión y refracción
A partir de las leyes de reflexión y refracción de la luz podemos prever el cambio en la dirección de los rayos.
Reflexión y refracción
Podemos sintetizar las relaciones entre los ángulos incidente iˆ , reflejado, rˆfl , y refractado rˆfr , según:
iˆ=rˆfl n1⋅sin(iˆ)=n2⋅sin(rˆfl)
Reversibilidad
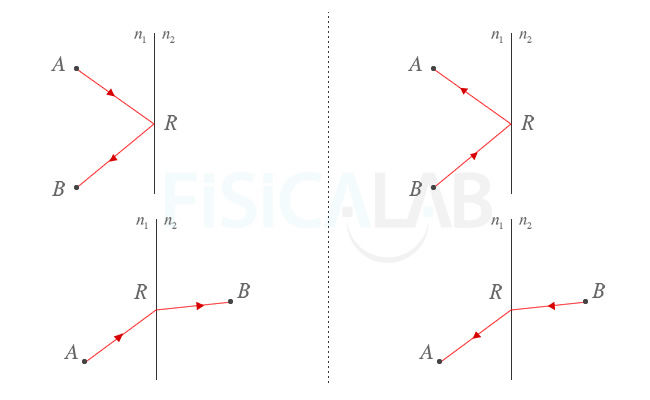
También conocida como ley de reciprocidad, esta ley o principio establece que la trayectoria de un rayo que parte de A y llega a B por una reflexión (o una refracción) en un punto R es la misma que la que tendría un rayo que partiese de B en sentido contrario, y se reflejase (o se refractase) en R, llegando a A. Veámoslo con una imagen:
Principio de reversibilidad.
Las dos imágenes superiores ilustran el principio de reversibilidad
en la reflexión y las dos imágenes inferiores en la refracción.

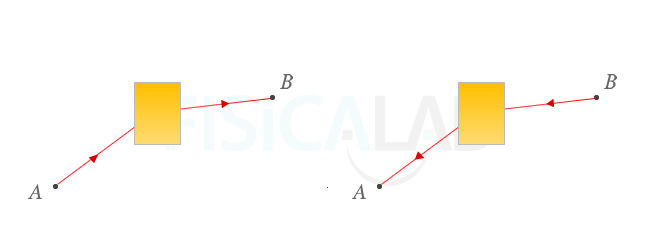
Principio de reversibilidad en sistemas complejos.
Cualquier sistema óptico complejo se puede sustituir por una 'caja
negra', en color naranja en la figura. La ley de reversibilidad que
aplicábamos a reflexiones y refracciones individuales también se puede
aplicar a sistemas ópticos complejos.
Luz monocromática
Despreciamos los efectos de la dispersión que la luz compuesta por varias longitudes de onda puede presentar.Absorción nula
En general, los medios absorben o difunden parte de los haces que propagan. Sin embargo nosotros no tendremos tampoco en cuenta este fenómeno.
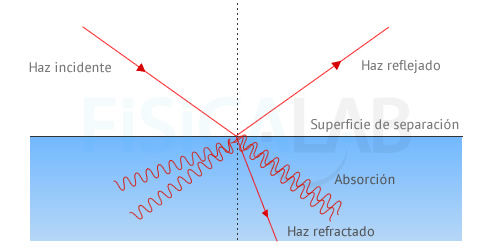
Absorción nula
Cuando un haz de luz real incide sobre una superficie de separación
con otro medio, parte del haz se refleja, otra parte se refracta, y otra
parte es absorvida por el propio medio, fenómeno este último que se
pone de manifiesto en el calentamiento que sufre la superficie. Nosotros
no tendremos en cuenta la absorción.
Elementos
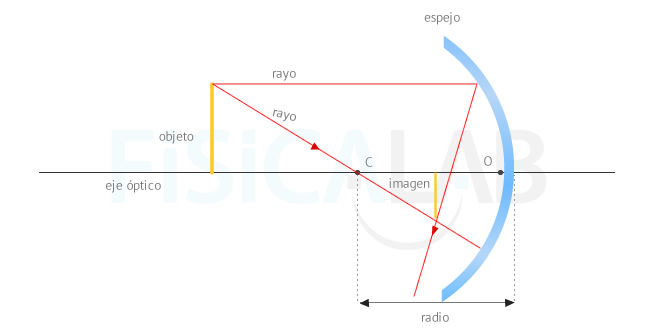
La óptica geométrica se basa en unos conceptos básicos que pasamos a detallar y que quedan recogidos en la siguiente imagen:
Elementos de la óptica geométrica
Sistema óptico con espejo que incluye los elementos principales que
debes conocer. La trayectoria de los rayos sería distinta si, en lugar
de un espejo (que es una superficie reflectora), hubiese un dioptrio
(que es una superficie refractora).
Objeto
En óptica geométrica llamamos objeto a cualquier fuente de la que proceden los rayos, bien sea por luz propia o reflejada. Los objetos pueden ser puntuales, cuando se supone todo su volumen concentrado en un único punto o no puntuales. En este último caso, cada punto de la superficie puede ser considerado en sí mismo una fuente puntual de rayos.Dioptrio
Es una superficie que separa dos medios transparentes de distinto índice de refracción. El dioptrio refracta la luz haciendo que los rayos varíen su trayectoria. Según su forma se distinguen:Espejo
Es una superficie lisa y pulimentada que refleja todos los rayos que llegan a ella. El espejo refleja la luz haciendo que los rayos varíen su trayectoria. Según su forma se distinguen:Centro de curvatura
Es el centro geométrico de la superficie esférica a la que pertenece el dioptrio o el espejo. En el caso de los dioptrios y espejos planos, se considera situado en el infinito. Solemos designarlo por la letra C.Radio de curvatura
Es el radio de la superficie esférica a la que pertenece el dioptrio o espejo. Podemos clasificar las superficies, en función de su curvatura en:
Superficies cóncavas y convexas
Espejos y dioptrios pueden ser tanto convexos (ilustración izquierda), como cóncavos (ilustración derecha).

| Criterio DIN (recomendado) | Criterio 2 | |||
| Convexo | Cóncavo | Convexo | Cóncavo | |
| Dioptrio | R > 0 | R < 0 | R > 0 | R < 0 |
| Espejo | R > 0 | R < 0 | R < 0 | R > 0 |
Sistema óptico
Se suele denominar sistema óptico al conjunto de varios dioptrios y espejos. Así, podemos distinguir:- Dióptricos: Si están formados sólo por dioptrios, es decir, superficies refractantes. De ellos, las lentes delgadas son los que estudiaremos con más atención
- Catóptricos: Si están formados sólo por espejos, es decir, superficies reflectantes
- Catadióptricos: Si están formados por ambos tipos de superficies
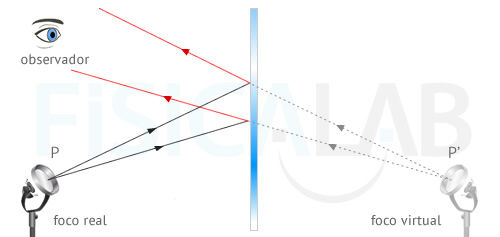
Imagen
Presta atención a la siguiente figura:
Imagen en espejo
La superficie azulada de la figura es un espejo que refleja todos los
rayos de luz que llegan a él. Un objeto luminoso, P, proyecta rayos
que, al reflejarse, son percibidos por un observador como si proviniesen
de P': El cerebro sitúa su posición prolongando en linea recta, hacia
atrás, los rayos que le llegan. Por eso, decimos que P' es la imagen de
P.
- Atendiendo a su orientación:
- Derecha : Tiene la misma orientación
- Invertida : Tiene la orientación contraria
- Atendiendo a su tamaño:
- Aumentada : Es más grande que el objeto
- Tamaño natural : Es tan grande como el objeto
- Disminuida : Es más pequeña que el objeto
- Atendiendo a la procedencia de los rayos:
- Real : Se forma por la intersección de los rayos convergentes que provienen del objeto, tras pasar por el sistema óptico. En un espejo aparecen delante y en un dioptrio detrás
- Virtual : Se forma por la intersección de las prolongaciones de los rayos divergentes que provienen del objeto, tras pasar por el sistema óptico. En un espejo están detrás y en un dioptrio delante

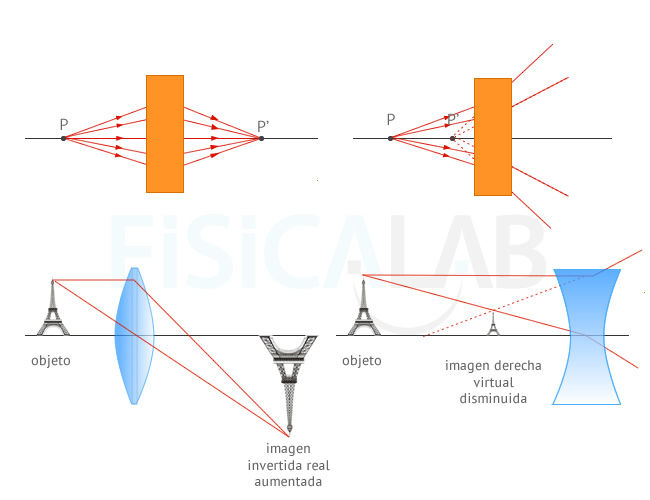
Tipos de imagen
Las dos figuras superiores ilustran claramente la diferencia entre
imagen real y virtual. A la izquierda, los rayos procedentes del objeto
convergen, tras pasar por el sistema óptico, en el punto P', que se
considera la imagen de P. En el segundo caso, los rayos, tras pasar por
el sistema óptico, divergen, por lo que la imagen P' se forma a partir
de la intersección de las prolongaciones de dichos rayos.
Las ilustraciones inferiores muestran, además, la diferencia entre imagen invertida/derecha y aumentada/disminuida para objetos no puntuales.
Las ilustraciones inferiores muestran, además, la diferencia entre imagen invertida/derecha y aumentada/disminuida para objetos no puntuales.
Eje óptico
También llamado eje principal, es el eje de simetría en torno al cual se sitúan el/los dioptrio/s y/o el/los espejo/s.Vértice óptico
También denominado centro óptico o polo, es el punto de corte del dioptrio o espejo con el eje óptico. Se suele denotar por la letra O ya que constituye el origen de coordenadas.UNIDAD14
UNIDAD 14 - DINAMICA DE LOS FLUIDOS
Unidad14 fisica de Paola Cecilia Catán
Ejemplo:
Determinar la velocidad del agua en ambos tramos de la tubería, sabiendo que:
S1=p (0.2)2 m2, S2=p (0.05)2 m2, r =1000 kg/m3, y p1-p2=1275 Pa.
Empleando la expresión anterior, obtenemos el valor de v2=1.6 m/s. Calculamos v1 a partir de la ecuación de continuidad (v1S1=v2S2) obteniendo v1=0.1 m/s ó 10 cm/s.
Podemos comprobarlo en el programa interactivo introduciendo los siguientes datos:
El valor de la velocidad en el tramo derecho se obtiene aplicando la ecuación de continuidad. Si el radio del tramo izquierdo es el doble que el radio del tramo derecho, la velocidad en el tramo derecho es cuatro veces mayor que en el izquierdo, es decir, mientras que la sección anterior S1 del elemento de fluido se desplaza10 cm, la sección posterior S2 se desplaza 40.
A continuación, nos fijaremos en los cambios energéticos.
A medida que el elemento de fluido (coloreado de amarillo) se mueve hacia la derecha su energía cambia. En la parte inferior izquierda del applet, se muestra la variación de energía cinética, de energía potencial y el trabajo de las fuerzas exteriores (que ejerce el resto del fluido sobre el elemento de fluido considerado). Las fuerzas exteriores se señalan mediante flechas. Como podemos comprobar la suma de las variaciones de energía cinética y potencial nos da el trabajo de las fuerzas exteriores.
Ejemplo:
Determinar la velocidad del agua en ambos tramos de la tubería, sabiendo que:
- Radio del tramo izquierdo de la tubería, 20 cm.
- Radio del tramo derecho de la tubería, 5 cm.
- Medida de la diferencia de presión, 1275 Pa.
S1=p (0.2)2 m2, S2=p (0.05)2 m2, r =1000 kg/m3, y p1-p2=1275 Pa.
Empleando la expresión anterior, obtenemos el valor de v2=1.6 m/s. Calculamos v1 a partir de la ecuación de continuidad (v1S1=v2S2) obteniendo v1=0.1 m/s ó 10 cm/s.
Podemos comprobarlo en el programa interactivo introduciendo los siguientes datos:
- Radio del tramo izquierdo de la tubería, 20 cm.
- Velocidad del fluido en el tramo izquierdo, 10 cm/s
- Diferencia de alturas entre los dos tramos, 0
Actividades
Se introduce- El radio del tramo izquierdo de la tubería, actuando en la barra de desplazamiento titulada Radio.
- El radio del tramo derecho está fijado en 5 cm.
- El valor de la velocidad del tramo izquierdo, actuando en la barra de desplazamiento titulada Velocidad.
- El desnivel, (un número positivo, nulo o negativo) o diferencia de alturas entre los dos tramos, en el control de edición titulado Desnivel.
El valor de la velocidad en el tramo derecho se obtiene aplicando la ecuación de continuidad. Si el radio del tramo izquierdo es el doble que el radio del tramo derecho, la velocidad en el tramo derecho es cuatro veces mayor que en el izquierdo, es decir, mientras que la sección anterior S1 del elemento de fluido se desplaza10 cm, la sección posterior S2 se desplaza 40.
A continuación, nos fijaremos en los cambios energéticos.
A medida que el elemento de fluido (coloreado de amarillo) se mueve hacia la derecha su energía cambia. En la parte inferior izquierda del applet, se muestra la variación de energía cinética, de energía potencial y el trabajo de las fuerzas exteriores (que ejerce el resto del fluido sobre el elemento de fluido considerado). Las fuerzas exteriores se señalan mediante flechas. Como podemos comprobar la suma de las variaciones de energía cinética y potencial nos da el trabajo de las fuerzas exteriores.
UNIDAD9
IMPULSO Y CANTIDAD DE MOVIMIENTO
Según el principio de masa, si a ésta se le aplica una fuerza F adquiere una aceleración a:
F = m.a
Siendo:
F: fuerza [F] = N (Newton)
a: aceleración [a] = m/s²
m: masa [m] = kg
Multiplicando ambos miembros por el tiempo T en que se aplica la fuerza F:
F.t = m.a.t
Como:
a.t = v
siendo:
v: velocidad [v] = m/s
t: tiempo [t] = s
Tenemos:
F.t = m.v
Al término F.t se lo denomina impulso de la fuerza y al término m.v se lo denomina cantidad de movimiento, entonces, para el primero:
I = F.t
siendo:
I: impulso [I] = kg.m/s
para el segundo:
p = m.v
siendo:
p: cantidad de movimiento [p] = kg.m/s
Para deducir las unidades, tenemos:
F.t = m.v
N.s = kg.m/s N = kg.m/s²
kg.m/s².s = kg.m/s
luego:
[I] = [p] = kg.m/s = N.s
El impulso de la fuerza aplicada es igual a la cantidad de movimiento que provoca, o dicho de otro modo, el incremento de la cantidad de movimiento de cualquier cuerpo es igual al impulso de la fuerza que se ejerce sobre él.
Unidades en los distintos sistemas
c.g.s.
|
S.I.
|
Técnico
| |
Cantidad de movimiento
Impulso
|
g.m/s
din.s
|
kg.m/s
N.s
|
kgf.s
kgf.s
|
El impulso y la cantidad de movimiento son magnitudes vectoriales.
Conservación de la cantidad de movimiento
Si con un cuerpo de masa m1 y velocidad v1 se aplica una fuerza a otro cuerpo de masa m2 y velocidad v2, como por ejemplo, en un saque de tenis, en ese instante es aplicable el principio de acción y reacción y tenemos que:
m1.v1 = m2.v2
es decir la masa de la raqueta por su velocidad, en el momento del choque, debe ser igual a la masa de la pelota de tenis por la velocidad que adquiere.
Enunciando la Ley de conservación de la cantidad de movimiento dice:
En cualquier sistema o grupo de cuerpos que interactúen, la cantidad de movimiento total, antes de las acciones, es igual a la cantidad de movimiento total luego de las acciones.
Σm.v = 0
mi.vi = mf.vf
ΔP = Δp1 + Δp2
Choque
Se produce choque entre dos cuerpos cuando uno de ellos encuentra en su trayectoria a otro y produciéndose contacto físico.
Al producirse el choque también se producen deformaciones en ambos cuerpos, éstas pueden desaparecer de inmediato o perdurar. Si las deformaciones desaparecen rápidamente significa que se ha producido un choque elástico, por el contrario, si permanecen se ha producido un choque inelástico o plástico.
En ambos casos ocurre una variación de la energía cinética que se transformará en calor que disiparán los cuerpos.
1) Choque plástico o inelástico
a) Velocidades de igual dirección y sentido
Supongamos un cuerpo 1 de masa m1 y velocidad v1 que se dirige a hacia el cuerpo 2 de masa m2 y velocidad v2, siendo ambas velocidades de igual dirección y sentido. Sobre cada cuerpo actuó en el momento del choque, el impulso que le provocó el otro cuerpo, entonces hay dos acciones de igual intensidad y sentido contrario, en consecuencia ambas cantidades de movimiento serán iguales y de sentido contrario. Luego del choque ambos cuerpos continúan juntos con una velocidad final común a ambos.
La velocidad final será:
m1.v1i + m2.v2i = m1.v1f + m2.v2f
como v1f y v2f son iguales porque ambos cuerpos siguen juntos:
v1f = v2f = vf
m1.v1i + m2.v2i = (m1 + m2).vf
vf = (m1.v1i + m2.v2i)/(m1 + m2)
b) Velocidades de igual dirección y sentido contrario.
En este caso los cuerpos poseían velocidades de igual dirección pero de sentido contrario antes del choque, como en el caso anterior luego del impacto continúan juntos, con una velocidad final que estará dada por la diferencia de las cantidades de movimiento. La velocidad final será:
m1.v1i - m2.v2i = m1.v1f + m2.v2f
igualmente:
v1f = v2f = vf
m1.v1i - m2.v2i = (m1 + m2).vf
vf = (m1.v1i - m2.v2i)/(m1 + m2)
La velocidad final mantendrá la misma dirección pero tendrá el sentido de la velocidad del cuerpo que antes del choque tenga más cantidad de movimiento.
2) Choque elástico
a) Velocidades de igual sentido
Durante el choque cada cuerpo recibe una cantidad de movimiento que es igual a la velocidad perdida por el otro. Al recuperar su forma inicial, cada uno pierde o gana respectivamente, la cantidad de movimiento ganada o perdida en el momento del choque, la velocidad final de cada uno será:
v1f = (v2f + v2i).m2/m1 + v1i
ó:
v1f = v2f + v2i - v1i
b) Velocidades de distinto sentido
En este caso los cuerpos literalmente rebotan, y la velocidad final de cada uno será:
v1f = (v2f - v2i).m2/m1 + v1i
El principio de conservación del impulso es el mismo que el de conservación de la cantidad de movimiento.
Cabe aclarar que en la práctica podemos aplicar el principio de conservación de la cantidad de movimiento durante los choques, siempre que el tiempo que dura el impacto sea muy pequeño.
Ejercicios resueltos de choque
Ejercicio 1
Los siguientes cuerpos chocan de forma elástica.Calcular la velocidad final V2.
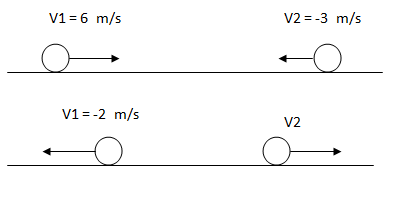
Solución
Como nos dicen que se trata de un choque elástico, sabemos que el coeficiente de restitución es igual a 1. Por lo tanto planteamos la fórmula del coeficiente de restitución y despejamos la velocidad del segundo cuerpo.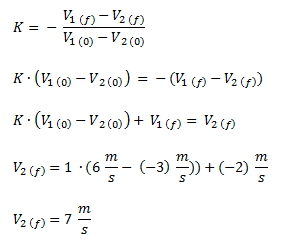
Ejercicio 2
Un cuerpo de 2 kg de masa se dirige en línea recta a 5 m/s hacia otro cuerpo de 3 kg que se encuentra detenido. Luego del choque ambos cuerpos quedan pegados.Calcular la velocidad final de los mismos.
Solución
Planteamos la fórmula de conservación de la cantidad de movimiento.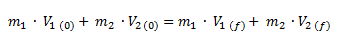
Como sabemos que ambos cuerpos quedan pegados, reemplazamos las dos velocidades finales por una sola (Vf).
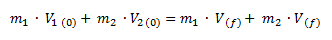
Despejamos la velocidad final del sistema y reemplazamos por los valores del ejercicio.
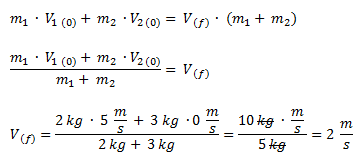
Ejercicio 3
Determinar la velocidad final de m2 y el tipo de choque.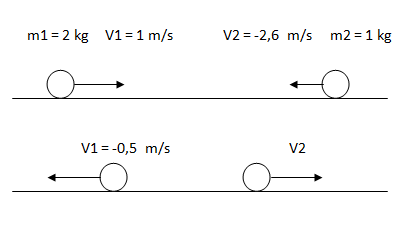
Solución
Planteamos la fórmula de conservación de la cantidad de movimiento y despejamos la velocidad final del segundo cuerpo.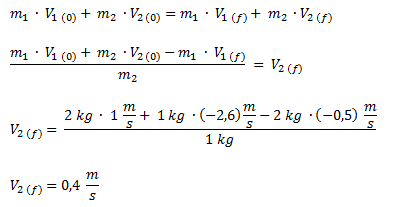
Para determinar el tipo de choque calculamos el coeficiente de restitución.
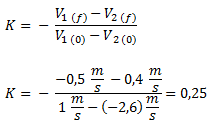
Como K es un valor mayor que cero y menor que uno, resulta un choque inelástico (o semielástico).
UNIDAD8
TRABAJO Y ENERGÍA
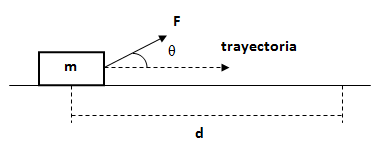
Trabajo: "Producto de la fuerza por el camino que recorre su punto de aplicación y por el coseno del ángulo que forma la una con el otro".
Energía : "Capacidad para realizar un trabajo".
Potencia: "Cantidad de energía producida o consumida por unidad de tiempo".
Trabajo de una fuerza
Una fuerza constante genera trabajo cuando, aplicada a un cuerpo, lo desplaza a lo largo de una determinada distancia.
Mientras se realiza trabajo sobre el cuerpo, se produce una transferencia de energía al mismo, por lo que puede decirse que el trabajo es energía en movimiento. Por otra parte, si una fuerza constante no produce movimiento, no se realiza trabajo. Por ejemplo, el sostener un libro con el brazo extendido no implica trabajo alguno sobre el libro, independientemente del esfuerzo necesario. El trabajo se expresa en Joules (J).
El trabajo realizado cuando la fuerza tiene la dirección de movimiento se expresa:
L = F.d
L: Trabajo realizado por la fuerza.
d: La distancia en la cual se aplicó la fuerza.
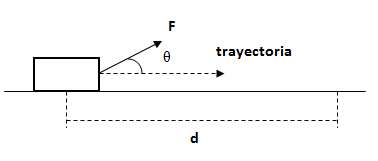
El trabajo realizado cuando la fuerza aplicada tiene una inclinación α con respecto al movimiento se expresa:
L = F.d.cos α
Para que una fuerza produzca trabajo dicha fuerza o una componente de la misma debe tener la dirección del movimiento o, dicho de otro modo, todas las fuerzas perpendiculares al movimiento no realizan trabajo.
La fuerza puede no ser mecánica,como ocurre en el levantamiento de un cuerpo o en la aceleración de un avión de reacción; también puede ser una fuerza electrostática, electrodinámica o de tensión superficial.
Energía
La magnitud denominada energía enlaza todas las ramas de la física. En el ámbito de la física, debe suministrarse energía para realizar trabajo. La energía se expresa en joules (J). Existen muchas formas de energía: energía potencial eléctrica y magnética, energía cinética, energía acumulada en resortes estirados, gases comprimidos o enlaces moleculares,energía térmica e incluso la propia masa.
Datos F = 15 N, θ = 35°, d = 2 m.
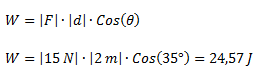
Datos m = 10 kg, F = 100 N, θ = 35°, d = 10 m, μd = 0,1.
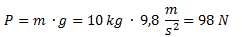
Calculamos el módulo de la fuerza normal, que en este caso es igual al peso ya que la superficie es horizontal y no hay otras fuerzas actuando.
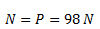
Calculamos el valor de la fuerza de rozamiento dinámico como el producto del coeficiente de rozamiento por la fuerza normal. También indicamos su módulo solamente.
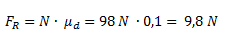
Finalmente calculamos el trabajo de las dos fuerzas.
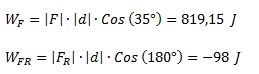
Lo planteamos como la suma de dos trabajos parciales: el correspondiente al tramo en el que la fuerza es variable (área de un triángulo) y el correspondiente al tramo en el que la fuerza es constante (área de un rectángulo).
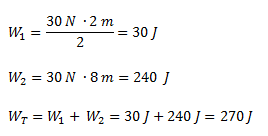
¿Cuál es el peso del bloque?
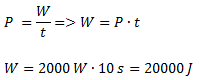
Planteamos la fórmula de trabajo y despejamos la fuerza, que es igual al peso.
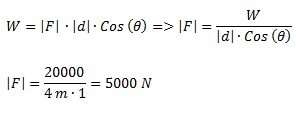
¿Cuál es el trabajo realizado por la bomba?
¿Cuál es la potencia empleada?
Datos: Peso específico del agua: 9800 N/m3.
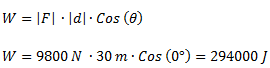
Para el cálculo de la potencia, convertimos los minutos a segundos, planteamos la fórmula de potencia y reemplazamos los valores.
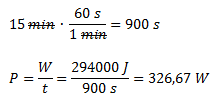
Hallar el trabajo realizado por las siguientes fuerzas: tensión de la cuerda, fuerza de rozamiento, peso, normal.
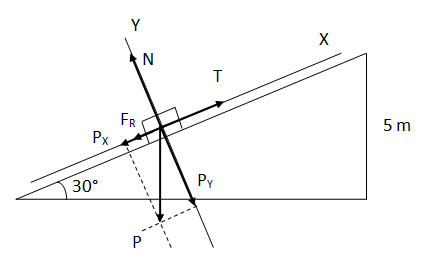
Calculamos el peso del bloque. Para simplificar las cuentas indicamos solo los módulos de las fuerzas y luego sumamos o restamos según el signo del esquema.
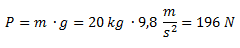
Calculamos las componentes del peso en los ejes X e Y.
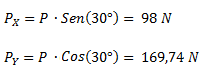
Planteamos la sumatoria de fuerzas en el eje Y. Despejamos la fuerza normal.
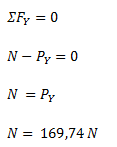
Calculamos la fuerza de rozamiento en base a la fuerza normal y al coeficiente de rozamiento.
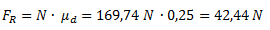
Planteamos la sumatoria de fuerzas en el eje X y despejamos la tensión de la cuerda.
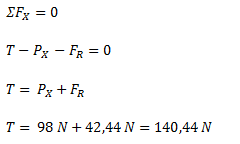
Calculamos la distancia sobre el plano (d) por medio de relaciones trigonométricas.
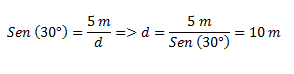
Finalmente calculamos el trabajo de cada fuerza, multiplicando los módulos de cada una de las fuerzas por la distancia recorrida y por el coseno del ángulo entre la fuerza y la trayectoria.
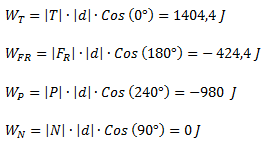
Calcular la potencia eléctrica generada, asumiendo una eficiencia del 100%.
Dato: Peso específico del agua = 9800 N/m3.
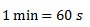
Planteamos la fórmula de potencia y reemplazamos al trabajo por el producto de la fuerza por la distancia.
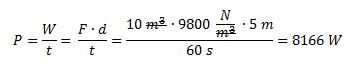
Ejercicios de trabajo
Ejercicio 1
Calcular el trabajo que realiza la fuerza F sobre la distancia d.Datos F = 15 N, θ = 35°, d = 2 m.

Solución
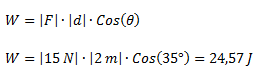
Ejercicio 2
Calcular el trabajo que realiza la fuerza F y la fuerza de rozamiento FR sobre la distancia d.Datos m = 10 kg, F = 100 N, θ = 35°, d = 10 m, μd = 0,1.

Solución
Calculamos el peso del bloque. Indicamos sólo su módulo: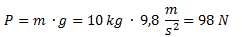
Calculamos el módulo de la fuerza normal, que en este caso es igual al peso ya que la superficie es horizontal y no hay otras fuerzas actuando.
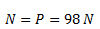
Calculamos el valor de la fuerza de rozamiento dinámico como el producto del coeficiente de rozamiento por la fuerza normal. También indicamos su módulo solamente.
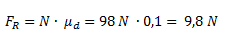
Finalmente calculamos el trabajo de las dos fuerzas.
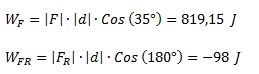
Ejercicio 4
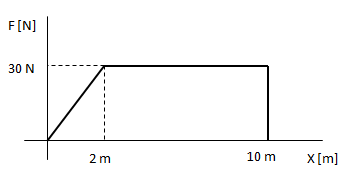
Calcular el trabajo de la siguiente fuerza.
Solución
El trabajo total realizado lo podemos calcular como el área bajo la curva.Lo planteamos como la suma de dos trabajos parciales: el correspondiente al tramo en el que la fuerza es variable (área de un triángulo) y el correspondiente al tramo en el que la fuerza es constante (área de un rectángulo).
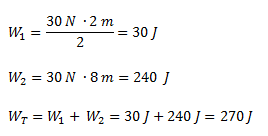
Ejercicio 5
Una grúa sube en forma vertical un bloque hasta una altura de 4 m, a velocidad constante y en un tiempo de 10 s. La potencia disipada para realizar ese trabajo es de 2000 W.¿Cuál es el peso del bloque?
Solución
Planteamos la fórmula de potencia y despejamos el trabajo realizado.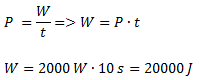
Planteamos la fórmula de trabajo y despejamos la fuerza, que es igual al peso.
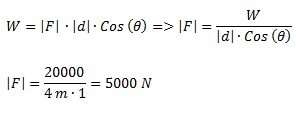
Ejercicio 6
Una bomba sube 1 m3 de agua a una altura de 30 m en 15 minutos.¿Cuál es el trabajo realizado por la bomba?
¿Cuál es la potencia empleada?
Datos: Peso específico del agua: 9800 N/m3.
Solución
Planteamos la fórmula de trabajo y reemplazamos por los valores del ejercicio: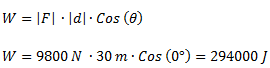
Para el cálculo de la potencia, convertimos los minutos a segundos, planteamos la fórmula de potencia y reemplazamos los valores.
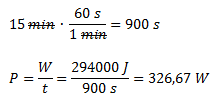
Ejercicio 7
Se sube un bloque de 20 kg por un plano inclinado de 30° y 5 metros de altura a través de una cuerda y a velocidad constante. El coeficiente de rozamiento dinámico entre el bloque y la superficie del plano es de 0,25.Hallar el trabajo realizado por las siguientes fuerzas: tensión de la cuerda, fuerza de rozamiento, peso, normal.
Solución
Hacemos un diagrama con la situación planteada en el ejercicio.
Calculamos el peso del bloque. Para simplificar las cuentas indicamos solo los módulos de las fuerzas y luego sumamos o restamos según el signo del esquema.
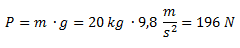
Calculamos las componentes del peso en los ejes X e Y.
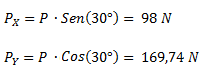
Planteamos la sumatoria de fuerzas en el eje Y. Despejamos la fuerza normal.
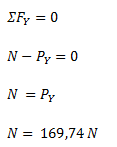
Calculamos la fuerza de rozamiento en base a la fuerza normal y al coeficiente de rozamiento.
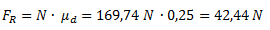
Planteamos la sumatoria de fuerzas en el eje X y despejamos la tensión de la cuerda.
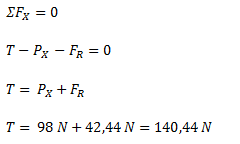
Calculamos la distancia sobre el plano (d) por medio de relaciones trigonométricas.
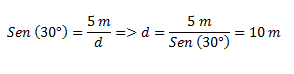
Finalmente calculamos el trabajo de cada fuerza, multiplicando los módulos de cada una de las fuerzas por la distancia recorrida y por el coseno del ángulo entre la fuerza y la trayectoria.
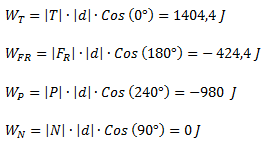
Ejercicio 8
Una presa tiene un caudal de 10 m3/min y una altura de 5 m.Calcular la potencia eléctrica generada, asumiendo una eficiencia del 100%.
Dato: Peso específico del agua = 9800 N/m3.
Solución
Pasamos el tiempo a unidades básica del Sistema Internacional.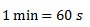
Planteamos la fórmula de potencia y reemplazamos al trabajo por el producto de la fuerza por la distancia.
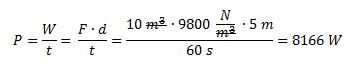
Suscribirse a:
Entradas (Atom)










