TRABAJO Y ENERGÍA
Trabajo: "Producto de la fuerza por el camino que recorre su punto de aplicación y por el coseno del ángulo que forma la una con el otro".
Energía : "Capacidad para realizar un trabajo".
Potencia: "Cantidad de energía producida o consumida por unidad de tiempo".
Trabajo de una fuerza
Una fuerza constante genera trabajo cuando, aplicada a un cuerpo, lo desplaza a lo largo de una determinada distancia.
Mientras se realiza trabajo sobre el cuerpo, se produce una transferencia de energía al mismo, por lo que puede decirse que el trabajo es energía en movimiento. Por otra parte, si una fuerza constante no produce movimiento, no se realiza trabajo. Por ejemplo, el sostener un libro con el brazo extendido no implica trabajo alguno sobre el libro, independientemente del esfuerzo necesario. El trabajo se expresa en Joules (J).
El trabajo realizado cuando la fuerza tiene la dirección de movimiento se expresa:
L = F.d
L: Trabajo realizado por la fuerza.
d: La distancia en la cual se aplicó la fuerza.
El trabajo realizado cuando la fuerza aplicada tiene una inclinación α con respecto al movimiento se expresa:
L = F.d.cos α
Para que una fuerza produzca trabajo dicha fuerza o una componente de la misma debe tener la dirección del movimiento o, dicho de otro modo, todas las fuerzas perpendiculares al movimiento no realizan trabajo.
La fuerza puede no ser mecánica,como ocurre en el levantamiento de un cuerpo o en la aceleración de un avión de reacción; también puede ser una fuerza electrostática, electrodinámica o de tensión superficial.
Energía
La magnitud denominada energía enlaza todas las ramas de la física. En el ámbito de la física, debe suministrarse energía para realizar trabajo. La energía se expresa en joules (J). Existen muchas formas de energía: energía potencial eléctrica y magnética, energía cinética, energía acumulada en resortes estirados, gases comprimidos o enlaces moleculares,energía térmica e incluso la propia masa.
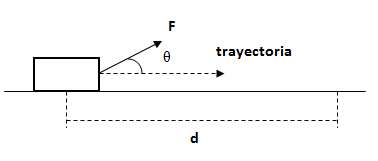
Datos F = 15 N, θ = 35°, d = 2 m.
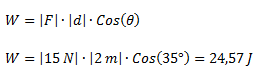
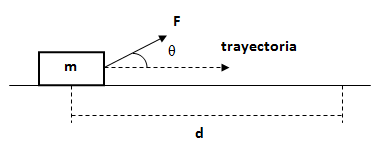
Datos m = 10 kg, F = 100 N, θ = 35°, d = 10 m, μd = 0,1.
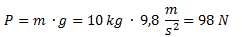
Calculamos el módulo de la fuerza normal, que en este caso es igual al peso ya que la superficie es horizontal y no hay otras fuerzas actuando.
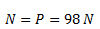
Calculamos el valor de la fuerza de rozamiento dinámico como el producto del coeficiente de rozamiento por la fuerza normal. También indicamos su módulo solamente.
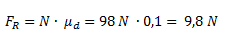
Finalmente calculamos el trabajo de las dos fuerzas.
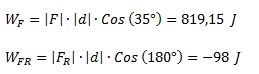
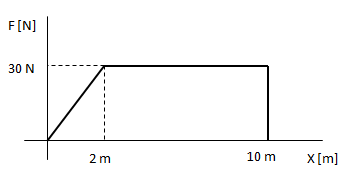
Lo planteamos como la suma de dos trabajos parciales: el correspondiente al tramo en el que la fuerza es variable (área de un triángulo) y el correspondiente al tramo en el que la fuerza es constante (área de un rectángulo).
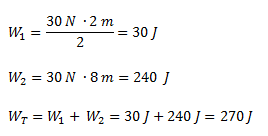
¿Cuál es el peso del bloque?
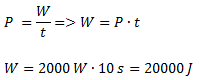
Planteamos la fórmula de trabajo y despejamos la fuerza, que es igual al peso.
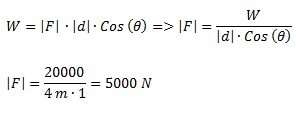
¿Cuál es el trabajo realizado por la bomba?
¿Cuál es la potencia empleada?
Datos: Peso específico del agua: 9800 N/m3.
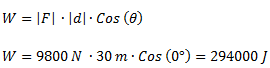
Para el cálculo de la potencia, convertimos los minutos a segundos, planteamos la fórmula de potencia y reemplazamos los valores.
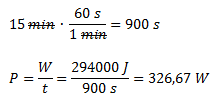
Hallar el trabajo realizado por las siguientes fuerzas: tensión de la cuerda, fuerza de rozamiento, peso, normal.
Calculamos el peso del bloque. Para simplificar las cuentas indicamos solo los módulos de las fuerzas y luego sumamos o restamos según el signo del esquema.
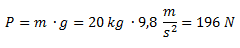
Calculamos las componentes del peso en los ejes X e Y.
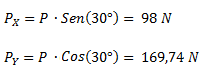
Planteamos la sumatoria de fuerzas en el eje Y. Despejamos la fuerza normal.
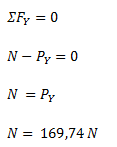
Calculamos la fuerza de rozamiento en base a la fuerza normal y al coeficiente de rozamiento.
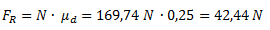
Planteamos la sumatoria de fuerzas en el eje X y despejamos la tensión de la cuerda.
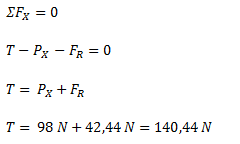
Calculamos la distancia sobre el plano (d) por medio de relaciones trigonométricas.
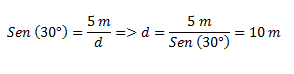
Finalmente calculamos el trabajo de cada fuerza, multiplicando los módulos de cada una de las fuerzas por la distancia recorrida y por el coseno del ángulo entre la fuerza y la trayectoria.
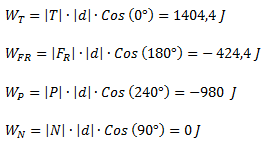
Calcular la potencia eléctrica generada, asumiendo una eficiencia del 100%.
Dato: Peso específico del agua = 9800 N/m3.
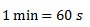
Planteamos la fórmula de potencia y reemplazamos al trabajo por el producto de la fuerza por la distancia.
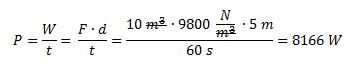
Ejercicios de trabajo
Ejercicio 1
Calcular el trabajo que realiza la fuerza F sobre la distancia d.Datos F = 15 N, θ = 35°, d = 2 m.

Solución
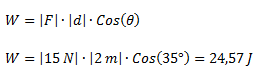
Ejercicio 2
Calcular el trabajo que realiza la fuerza F y la fuerza de rozamiento FR sobre la distancia d.Datos m = 10 kg, F = 100 N, θ = 35°, d = 10 m, μd = 0,1.

Solución
Calculamos el peso del bloque. Indicamos sólo su módulo: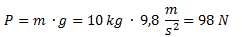
Calculamos el módulo de la fuerza normal, que en este caso es igual al peso ya que la superficie es horizontal y no hay otras fuerzas actuando.
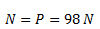
Calculamos el valor de la fuerza de rozamiento dinámico como el producto del coeficiente de rozamiento por la fuerza normal. También indicamos su módulo solamente.
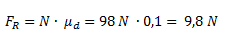
Finalmente calculamos el trabajo de las dos fuerzas.
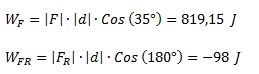
Ejercicio 4
Calcular el trabajo de la siguiente fuerza.
Solución
El trabajo total realizado lo podemos calcular como el área bajo la curva.Lo planteamos como la suma de dos trabajos parciales: el correspondiente al tramo en el que la fuerza es variable (área de un triángulo) y el correspondiente al tramo en el que la fuerza es constante (área de un rectángulo).
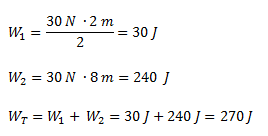
Ejercicio 5
Una grúa sube en forma vertical un bloque hasta una altura de 4 m, a velocidad constante y en un tiempo de 10 s. La potencia disipada para realizar ese trabajo es de 2000 W.¿Cuál es el peso del bloque?
Solución
Planteamos la fórmula de potencia y despejamos el trabajo realizado.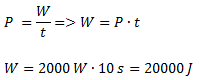
Planteamos la fórmula de trabajo y despejamos la fuerza, que es igual al peso.
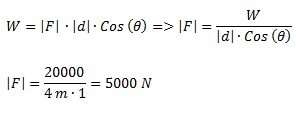
Ejercicio 6
Una bomba sube 1 m3 de agua a una altura de 30 m en 15 minutos.¿Cuál es el trabajo realizado por la bomba?
¿Cuál es la potencia empleada?
Datos: Peso específico del agua: 9800 N/m3.
Solución
Planteamos la fórmula de trabajo y reemplazamos por los valores del ejercicio: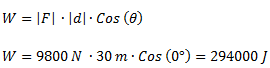
Para el cálculo de la potencia, convertimos los minutos a segundos, planteamos la fórmula de potencia y reemplazamos los valores.
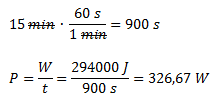
Ejercicio 7
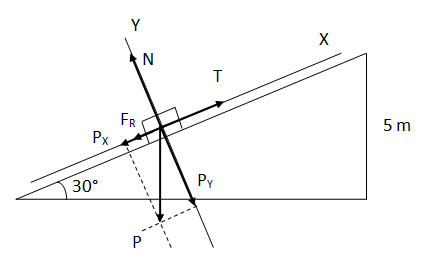
Se sube un bloque de 20 kg por un plano inclinado de 30° y 5 metros de altura a través de una cuerda y a velocidad constante. El coeficiente de rozamiento dinámico entre el bloque y la superficie del plano es de 0,25.Hallar el trabajo realizado por las siguientes fuerzas: tensión de la cuerda, fuerza de rozamiento, peso, normal.
Solución
Hacemos un diagrama con la situación planteada en el ejercicio.
Calculamos el peso del bloque. Para simplificar las cuentas indicamos solo los módulos de las fuerzas y luego sumamos o restamos según el signo del esquema.
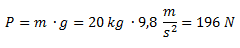
Calculamos las componentes del peso en los ejes X e Y.
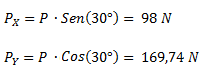
Planteamos la sumatoria de fuerzas en el eje Y. Despejamos la fuerza normal.
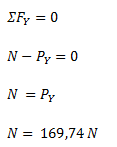
Calculamos la fuerza de rozamiento en base a la fuerza normal y al coeficiente de rozamiento.
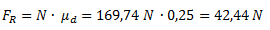
Planteamos la sumatoria de fuerzas en el eje X y despejamos la tensión de la cuerda.
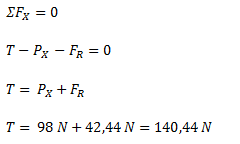
Calculamos la distancia sobre el plano (d) por medio de relaciones trigonométricas.
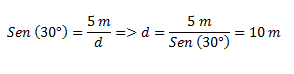
Finalmente calculamos el trabajo de cada fuerza, multiplicando los módulos de cada una de las fuerzas por la distancia recorrida y por el coseno del ángulo entre la fuerza y la trayectoria.
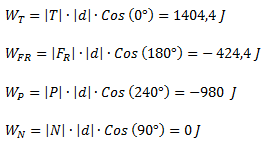
Ejercicio 8
Una presa tiene un caudal de 10 m3/min y una altura de 5 m.Calcular la potencia eléctrica generada, asumiendo una eficiencia del 100%.
Dato: Peso específico del agua = 9800 N/m3.
Solución
Pasamos el tiempo a unidades básica del Sistema Internacional.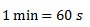
Planteamos la fórmula de potencia y reemplazamos al trabajo por el producto de la fuerza por la distancia.
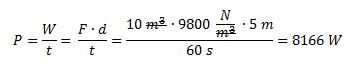
No hay comentarios:
Publicar un comentario