Hidrostática
El principio de Pascal y sus aplicaciones
La presión aplicada en un punto de un líquido contenido en un recipiente se transmite con el mismo valor a cada una de las partes del mismo. Este enunciado, obtenido a partir de observaciones y experimentos por el físico y matemático francés Blaise Pascal (1623-1662), se conoce como principio de Pascal.
El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter incompresible de los líquidos. En esta clase de fluidos la densidad es constante, de modo que de acuerdo con la ecuación p = p0 + ρ.g.h si se aumenta la presión en la superficie libre, por ejemplo, la presión en el fondo ha de aumentar en la misma medida, ya que ρ.g.hno varía al no hacerlo h.
La prensa hidráulica constituye la aplicación fundamental del principio de Pascal y también un dispositivo que permite entender mejor su significado. Consiste, en esencia, en dos cilindros de diferente sección comunicados entre sí, y cuyo interior está completamente lleno de un líquido incompresible que puede ser agua o aceite. Dos émbolos de secciones diferentes se ajustan, respectivamente, en cada uno de los dos cilindros, de modo que estén en contacto con el líquido. Cuando sobre el émbolo de menor sección A1 se ejerce una fuerza F1 la presión p1 que se origina en el líquido en contacto con él se transmite íntegramente y de forma instantánea a todo el resto del líquido; por tanto, será igual a la presión p2 que ejerce el líquido sobre el émbolo de mayor sección A2, es decir:
p1 = p2 ⇒ F1/A1 = F2/A2 ⇒ F1 = F2.A1/A2
Si la sección A2 es veinte veces mayor que la A1, la fuerza F1 aplicada sobre el émbolo pequeño se ve multiplicada por veinte en el émbolo grande. La prensa hidráulica es una máquina simple semejante a la palanca de Arquímedes, que permite amplificar la intensidad de las fuerzas y constituye el fundamento de elevadores, prensas, frenos y muchos otros dispositivos hidráulicos de maquinaria industrial.
Observación del principio de los vasos comunicantes. Diversas formas de recipientes. "El nivel de un líquido contenido en recipientes de diferentes formas comunicados entre sí, se mantiene a igual altura"
Principio de Arquímedes (Empuje)
El segundo principio importante de la estática de fluidos fue descubierto Arquímedes. Cuando un cuerpo está total o parcialmente sumergido en un fluido en reposo, el fluido ejerce una presión sobre todas las partes de la superficie del cuerpo que están en contacto con el fluido. La presión es mayor sobre las partes sumergidas a mayor profundidad. La resultante de todas las fuerzas es una dirigida hacia arriba y llamada el empuje sobre el cuerpo sumergido.
Un cuerpo total o parcialmente sumergido en un fluido es empujado hacia arriba con una fuerza que es igual al peso del fluido desplazado por dicho cuerpo.
Empuje y fuerza ascencional:
E = δ.g.Vd
Fa = E - P
Fa = δ.g.Vd - m.g
E: Empuje (N).
Fa: Fuerza ascencional (N).
P: Peso del cuerpo (N).
Vd: Volumen desplazado por el cuerpo (m³).
δ: Densidad del fluido (kg/m³).
g: Aceleración de la gravedad (m/s²).
Esto explica por qué flota un barco muy cargado; su peso total es exactamente igual al peso del agua que desplaza, y ese agua desplazada ejerce la fuerza hacia arriba que mantiene el barco a flote.
Si E > P ⇒ Fa > 0, el cuerpo flota.
Si E < P ⇒ Fa < 0, el cuerpo se hunde.
Si E = P ⇒ Fa = 0, el cuerpo permanece estático.
El punto sobre el que puede considerarse que actúan todas las fuerzas que producen el efecto de flotación se llama centro de flotación, y corresponde al centro de gravedad del fluido desplazado. El centro de flotación de un cuerpo que flota está situado exactamente encima de su centro de gravedad. Cuanto mayor sea la distancia (d) entre ambos, mayor es la estabilidad del cuerpo.
Peso aparente
Un cuerpo que flota en un fluido aparenta ser más liviano que si está colocado sobre suelo firme a nivel del mar, en éste caso se habla de peso aparente, y es:
Pa = P - E
Se trata de una fuerza igual a la fuerza ascensional pero opuesta.
Fa = Pa
Ejercicios resueltos de hidrostática
Ejercicio 1
¿Cuál es la presión que soporta un buzo sumergido a 10 metros de profundidad en el mar?Datos: Densidad del agua de mar = 1,025 kg/L. Presión atmosférica 101325 Pa.
Solución
Primero convertimos las unidades dadas en el ejercicio a unidades del Sistema Internacional: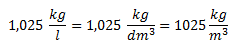
Luego aplicamos la definición de presión hidrostática, considerando la presión atmosférica.
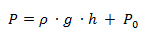
Reemplazamos los valores del ejercicio en la fórmula:
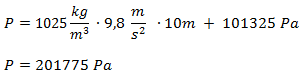
Ejercicio 2
Un submarino experimenta una presión de 4 atm bajo el agua de mar.¿A qué profundidad se encuentra sumergido?
Datos: Densidad del agua de mar = 1,025 kg/L. Presión atmosférica = 1 atm = 101325 Pa.
Solución
Lo primero que hacemos, como siempre, es convertir los valores dados a unidades del SI.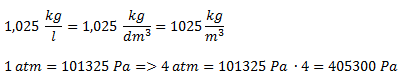
Luego planteamos la ecuación de presión hidrostática y despejamos la altura:
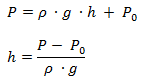
Reemplazamos por los valores dados en el ejercicio y obtenemos la altura:
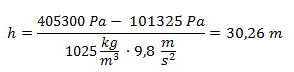
Ejercicio 3
¿Cuál es la fuerza ejercida sobre una chapa cuadrada de 30 cm de lado que se encuentra en el fondo de un tanque de agua lleno hasta 1,5 m, sin considerar la presión atmosférica?Datos: Densidad del agua = 1 kg/dm3.
Solución
Pasamos las unidades al SI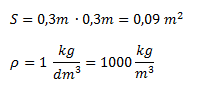
Planteamos la ecuación de la presión hidrostática:
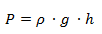
Reemplazamos por los valores dados:
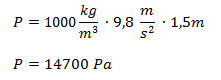
Planteamos la fórmula de presión y despejamos la fuerza:
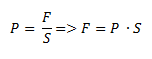
Reemplazamos por los valores dados en el ejercicio:
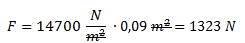
Ejercicio 4
Determinar la fuerza que equilibra el sistema, sabiendo que las superficies s1 y s2 tienen diámetros circulares de 10 y 40 cm respectivamente.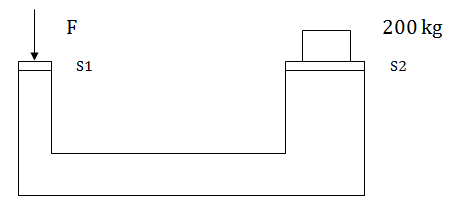
Solución
Convertimos los valores dados a las unidades básicas del SI y calculamos los radios: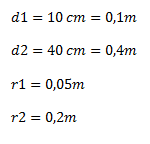
Calculamos las superficies s1 y s2 en función de los radios:
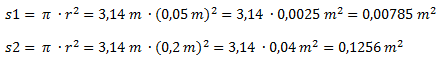
Calculamos la fuerza que ejerce la masa en s2. Para eso utilizamos la fórmula de peso.
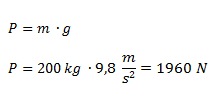
Planteamos la ecuación de la prensa hidráulica reemplazando a la fuerza 1 por F y a la fuerza 2 por el peso.
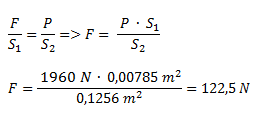
Ejercicio 5
¿Cuál es la diferencia de presión que existe entre dos puntos bajo el agua que se encuentran separados verticalmente por 1 m? Dato: Densidad del agua = 1000 kg/m3.Solución
Para resolver este ejercicio en primer lugar calculamos el peso específico del agua en base a su densidad. Para ello multiplicamos la densidad por la aceleración de la gravedad: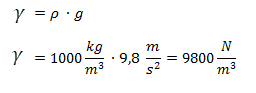
Luego aplicamos el teorema fundamental de la hidrostática que nos indica que la diferencia de presión entre dos puntos es igual al peso específico multiplicado por la diferencia de altura.
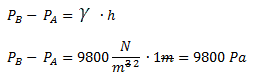
Ejercicio 6
Dado el tubo en U de la figura, determinar la diferencia de altura entre los líquidos sabiendo que la columna a tiene una altura de 25 cm, la densidad del líquido de la columna a es de 800 kg/m3 y que la columna b contiene agua con densidad 1000 kg/m3.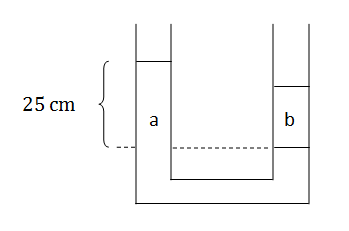
Solución
Indicamos nombres para cada una de las alturas: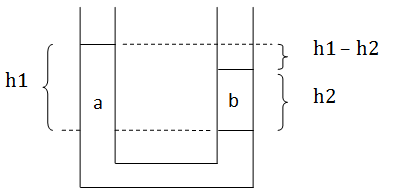
Pasamos las unidades al SI:
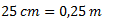
Sabemos que para que el sistema esté en equilibrio la presión hidrostática debe ser la misma en la isobara. La presión hidrostática la podemos calcular como el producto de la densidad, por la gravedad y por la altura.
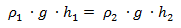
Despejamos la altura de la segunda columna:
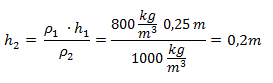
Luego la diferencia de alturas la calculamos con la diferencia entre la altura de cada una de las dos columnas:
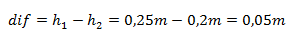


No hay comentarios:
Publicar un comentario